堆算法总结

阅读本篇需要对二叉树及其结构有基本的了解。

概念

堆一定是一颗完全二叉树, 按排序大小规则主要分为 2 种类型————最大堆和最小堆。

• 最大堆：根节点的值大于等于左右子节点的值。
• 最小堆：根节点的值小于等于左右子节点的值。

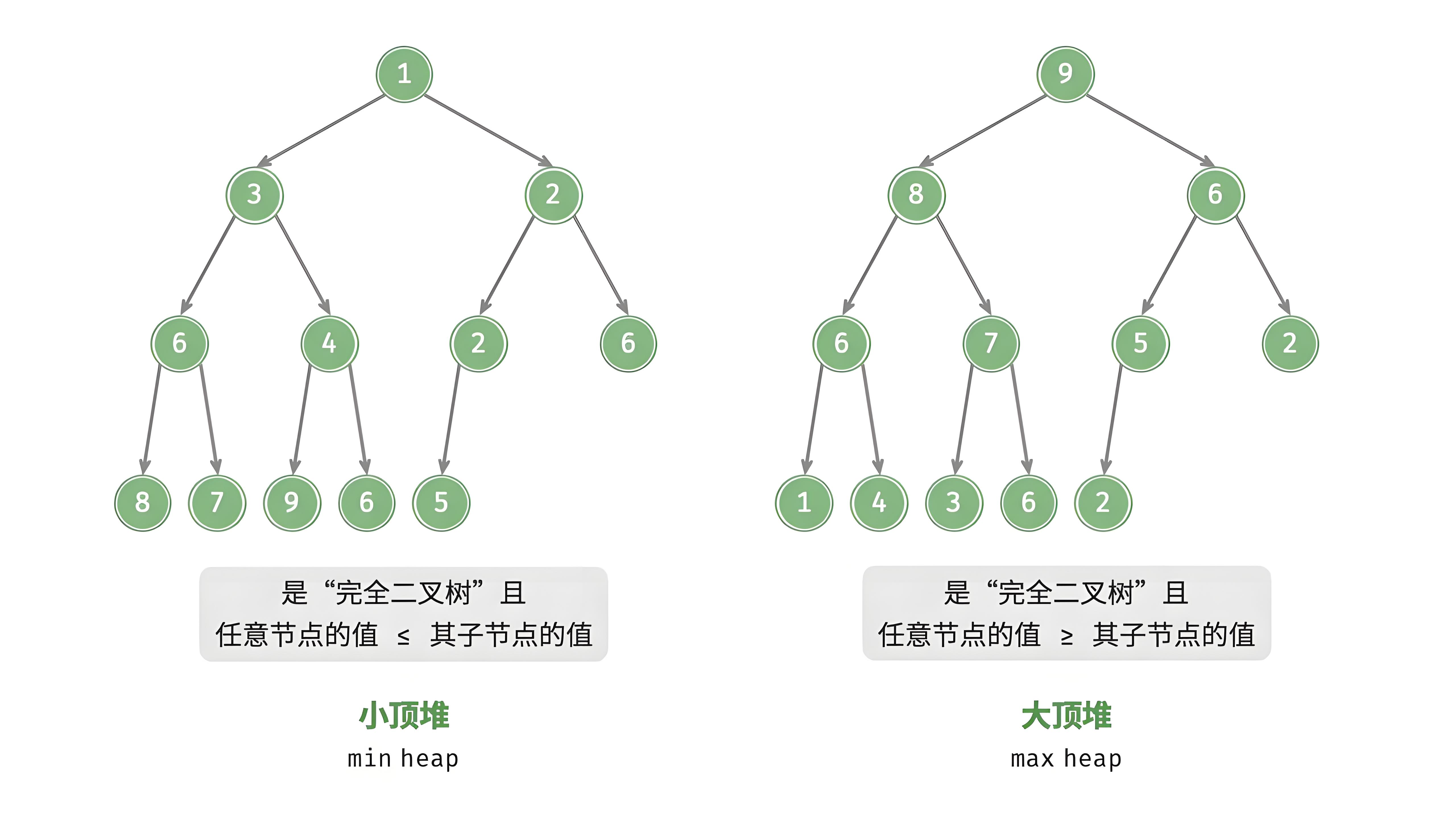
总结：最大堆和最小堆的根本区别在于根节点的最值情况。

Heap 类设计

在堆算法解题中，一般都需要设计一个 Heap 类，用于实现最大堆和最小堆的通用操作。

成员变量设计

在堆排序中仅需要一个数组结构，用于表达二叉树即可。

• heapArr = []

操作方法设计

在实际书写中应当遵循由基础工具方法到具体逻辑方法的顺序。

工具方法：

• getParentIndex(i): 获取父节点索引

getParentIndex(i) {
  return Math.floor((i - 1) / 2);
}

• getLeftChildIndex(i): 获取左子节点索引

getLeftChildIndex(i) {
  return 2 * i + 1;
}

• getRightChildIndex(i): 获取右子节点索引

getRightChildIndex(i) {
  return 2 * i + 2;
}

• size(): 堆元素的数量

size() {
  return this.heapArr.length;
}

• peek(): 访问堆顶元素（注意是访问，不是取出）

peek() {
  return this.heapArr[0];
}

• swap(i，j): 交换堆中的两个元素

swap(i, j) {
  const temp = this.heapArr[i];
  this.heapArr[i] = this.heapArr[j];
  this.heapArr[j] = temp;
}

有了以上几个工具方法之后，接下来开始考虑建堆的核心操作。

堆化的过程主要分 2 种情况——自上而下堆化、自下而上堆化。
这里以最大堆为例：

• siftDown: 自上而下堆化

siftDown(i) {
  while (true) {
    // 分别获取左右节点索引
    const leftIndex = this.getLeftChildIndex(i);
    const rightIndex = this.getRightChildIndex(i);
    // 最大值的索引
    let maxIndex = i;
    // 如果有左节点且左节点大于当前节点，则更新最大值索引
    if (leftIndex < this.size() && this.heapArr[leftIndex] > this.heapArr[maxIndex]) {
      maxIndex = leftIndex;
    }
    // 如果有右节点且右节点大于当前节点，则更新最大值索引
    if (rightIndex < this.size() && this.heapArr[rightIndex] > this.heapArr[maxIndex]) {
      maxIndex = rightIndex;
    }
    // maxIndex 没发生交换,则结束
    if (maxIndex === i) {
      break;
    }
    // 如果maxIndex 发生了交换，则交换当前节点和最大值节点, 继续循环
    this.swap(i, maxIndex);
    i = maxIndex;
  }
}

自上而下堆化目的是从根节点开始，依次比较当前节点和左右子节点，将较大的值与当前节点交换，然后继续比较交换后的节点。

• siftUp: 自下而上堆化

siftUp(i) {
  while (i > 0) {
    const parentIndex = this.getParentIndex(i);
    if (this.heapArr[i] <= this.heapArr[parentIndex]) {
      break;
    }
    // 如果当前元素大于父节点，则交换
    this.swap(i, parentIndex);
    i = parentIndex;
  }
}

自下而上堆化目的是从叶子节点开始，依次比较当前节点和父节点，将较小的值与当前节点交换，然后继续比较交换后的节点。

• push: 往堆中追加元素

push(val) {
  this.heapArr.push(val);
  this.siftUp(this.size() - 1);
}

在往堆中追加一个元素时，会从完全二叉树的末尾插入，然后通过自下而上堆化操作将其移动到合适位置。

• pop: 堆顶元素出堆

pop() {
  if (this.size() === 1) {
    return this.heapArr.pop();
  }
  // 交换堆顶元素和最后一个元素
  const result = this.heapArr[0];
  this.heapArr[0] = this.heapArr.pop();
  this.siftDown(0);
  return result;
}

在从堆中取出一个元素时，为了尽可能减少交换次数，将堆顶元素和最后一个元素交换，然后再对堆顶元素进行自上而下堆化操作将其移动到合适位置。

如果允许初始化的时候传入一个未进行堆化的数组, 那个在类的 construct 中需要从最后一个父节点开始, 依次自上而下进行堆化。

constructor(nums = []) {
  if (nums.length) {
    this.heapArr = nums;
    // 自下而上堆化(除叶节点以外的其他所有节点)
    for (let i = this.getParentIndex(nums.length-1); i >= 0; i--) {
      this.siftDown(i)
    }
  }
}

至此，堆的常用操作已经全部实现了。 完整代码：

class Heap {
  heapArr = []

  constructor(nums = []) {
    if (nums.length) {
      this.heapArr = nums;
      // 自下而上堆化(除叶节点以外的其他所有节点)
      for (let i = this.getParentIndex(nums.length-1); i >= 0; i--) {
        this.siftDown(i)
      }
    }
  }

  /**
   * 获取父节点
   * @param i
   * @return {number}
   */
  getParentIndex(i) {
    return Math.floor((i - 1) / 2);
  }

  /**
   * 获取左子节点
   * @param i
   * @return {number}
   */
  getLeftChildIndex(i) {
    return 2 * i + 1;
  }

  /**
   * 获取右子节点
   * @param i
   * @return {number}
   */
  getRightChildIndex(i) {
    return 2 * i + 2;
  }

  /**
   * 堆元素数量
   * @return {number}
   */
  size() {
    return this.heapArr.length;
  }

  /**
   * 访问堆顶元素
   */
  peek() {
    return this.heapArr[0];
  }

  /**
   * 元素入堆
   */
  push(val) {
    this.heapArr.push(val);
    this.siftUp(this.size() - 1);
  }

  /**
   * 从低到顶堆化
   */
  siftUp(i) {
    while (i > 0) {
      const parentIndex = this.getParentIndex(i);
      if (this.heapArr[i] <= this.heapArr[parentIndex]) {
        break;
      }
      this.swap(i, parentIndex);
      i = parentIndex;
    }
  }

  /**
   * 从顶到低堆化
   * @param i
   */
  siftDown(i) {
    while (true) {
      const leftIndex = this.getLeftChildIndex(i);
      const rightIndex = this.getRightChildIndex(i);
      let maxIndex = i;
      if (leftIndex < this.size() && this.heapArr[leftIndex] > this.heapArr[maxIndex]) {
        maxIndex = leftIndex;
      }
      if (rightIndex < this.size() && this.heapArr[rightIndex] > this.heapArr[maxIndex]) {
        maxIndex = rightIndex;
      }
      // maxIndex 没发生交换,则结束
      if (maxIndex === i) {
        break;
      }
      this.swap(i, maxIndex);
      i = maxIndex;
    }
  }

  /**
   * 交换堆中两个元素
   * @param i
   * @param j
   */
  swap(i, j) {
    const temp = this.heapArr[i];
    this.heapArr[i] = this.heapArr[j];
    this.heapArr[j] = temp;
  }

  /**
   * 堆顶元素出堆
   * @return {*}
   */
  pop() {
    if (this.size() === 1) {
      return this.heapArr.pop();
    }
    // 交换堆顶元素和最后一个元素
    const result = this.heapArr[0];
    this.heapArr[0] = this.heapArr.pop();
    this.siftDown(0);
    return result;
  }
}

解决的问题

Top-k 问题

Top-k 问题涉及从一组数据中找到最大的 k 个元素（或最小的 k 个元素）。

核心思路: 如果要求由大到小第 K 个, 则建立一个容量为 K 的小顶堆, 从头开始遍历, 不断以大的值替换掉堆顶元素, 遍历完成堆顶就是目标值。反则反之。

如：Leetcode 347. 前 K 个高频元素